Oral Abstract 3: Scanner-specific simulation and reduction of eddy-current effects in cardiac DTI

Diffusion-encoding gradients in second-order motion-compensated cardiac DTI (cDTI) can cause significant eddy currents (EC), compromising image quality^1,2. In this work, the EC response in cDTI is analyzed and its effects are minimized using realistic scanner-specific simulations and tailored sequence gaps.

Methods: Scanner-specific cDTI EC simulations were implemented based on the open-source Python package CMRsim³. The simulation module allows the calculation of EC effects up to the second spatial order based on a measured gradient modular transfer function (GMTF). The GMTF can be measured using image-based approaches⁴ or a dynamic field camera⁵. Extracting the sequence-specific response in the Fourier space allows the calculation of time-resolved EC fields, as illustrated in Figure 1.

The EC module further allows to investigate the evolution of longitudinal and transversal magnetization throughout the sequence. The magnetization can be simulated at any sequence step for combined or individual orders of EC effects. Figure 2 shows the effects of the 0^th, 1^st, and 2^nd order eddy currents on the phase of the transversal magnetization for the cDTI encoding sequence shown in Figure 1 with a diffusion encoding of 450 s/mm² in x direction and an EC gap of 0 ms. The phase is extracted prior to the tip-up pulse.

Furthermore, integration of the EC module in CMRsim allows the simulation of a full k-space readout. To this end, cDTI encoding was combined with a single-shot Cartesian balanced steady-state free precession (bSSFP) readout⁶. The simulation was repeated twice, once with a tip-up pulse of phase 0° and once with a tip-up pulse of phase 90°. Accordingly, the image phase due to diffusion gradient-related ECs could be captured. Subsequently, the EC gap was changed, and the simulated EC prediction was validated using measured data acquired on the real system (3T Philips; 95 mT/m at 200 T/m/s).

Results:

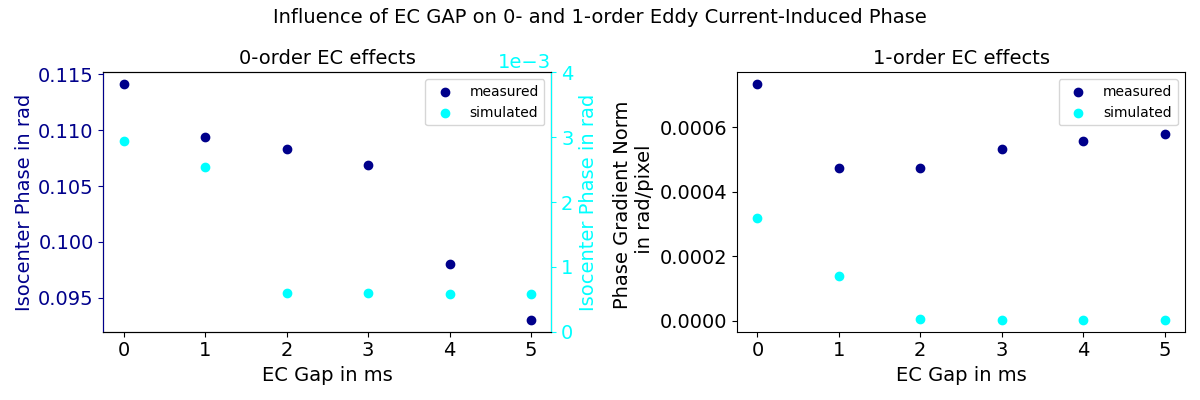
A significant reduction of EC effects was observed when inserting an EC gap of at least 1 ms between the end of the diffusion gradients and the beginning of the tip-up pulse, as shown in Figure 3. A similar effect was observed in measurement data acquired on a static phantom.

Differences between the simulated and measured data arise from neglecting eddy currents and noise in the bSSFP readout simulation and from potentially underestimating primarily zero- and second-order EC effects due to smoothing of the noisy GMTF.

Conclusion:

In summary, the developed CMRsim EC module allows in-depth analysis of EC effects in cDTI based on measured GMTF data. It has been demonstrated that short gaps in the sequence design can help to reduce EC effects. More considerations, such as the EC effects on the readout sequence, noise, potential compensation mechanisms and the impact of motion, remain to be investigated.

Figure 1: The EC simulation module uses the CMRsim framework and the sequence-independent scanner-specific GMTF to simulate the eddy current effects of a cDTI sequence up to the second spatial order.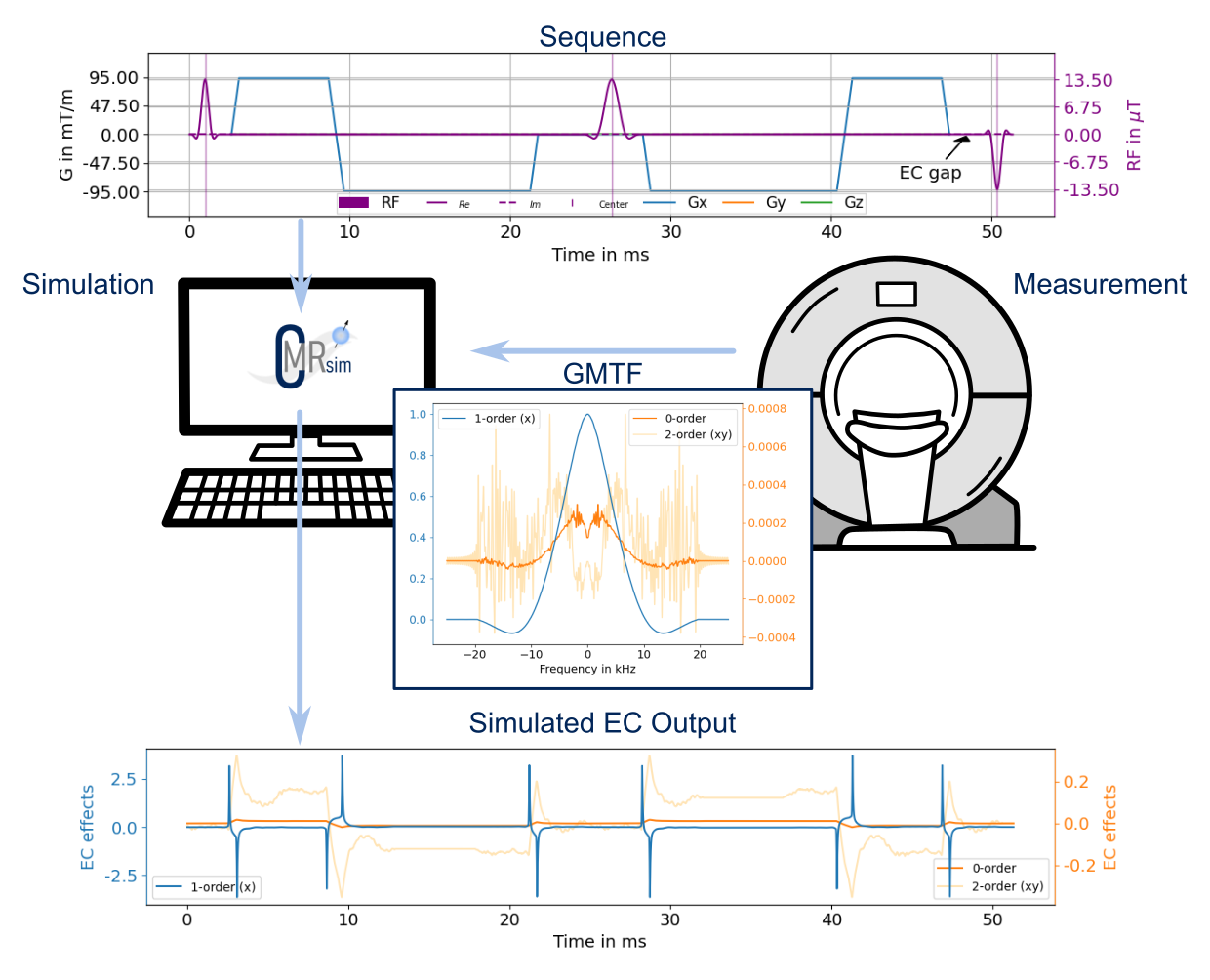

Figure 2: The 0th, 1st and 2nd-order EC effects on the phase of the transverse magnetization prior to the tip-up pulse observed for a DTI encoding of 450 s/mm2 in x direction.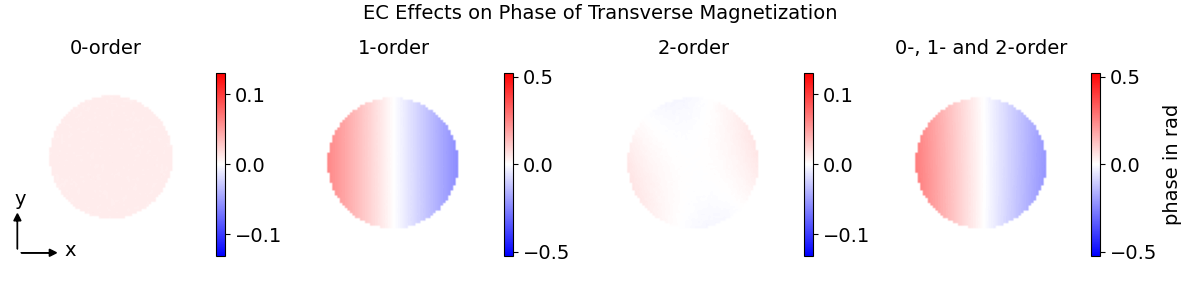

Figure 3: The isocenter phase corrected with the isocenter phase with no applied DTI gradients as an approximation for the gap dependence of the 0th-order EC-induced phase (left). The mean phase gradient norm of a 60-pixel isocentric circle as an approximation for the gap dependence of the 1st-order EC-induced phase ramp strength (right).